Ensemble-Methoden im maschinellen Lernen: Bagging & Subagging


In diesem Blogbeitrag werden wir den Bagging-Algorithmus sowie eine rechnerisch effizientere Variante davon, das Subagging, untersuchen. Mit kleinen Modifikationen sind diese Algorithmen auch unter dem Namen Random Forest bekannt und werden hier bei statworx, in der Industrie und in der Wissenschaft, weit verbreitet eingesetzt.
Fast alle statistischen Vorhersage- und Lernprobleme stehen vor einem Bias-Varianz-Kompromiss. Dies ist insbesondere bei sogenannten instabilen Prädiktoren ausgeprägt. Während sie aufgrund ihrer flexiblen Anpassung an die Daten verzerrungsarme Schätzungen liefern, reagieren solche Prädiktoren sehr empfindlich auf kleine Veränderungen im zugrunde liegenden Datensatz und weisen daher eine hohe Varianz auf. Ein häufig genanntes Beispiel sind Regressionsbaum-Prädiktoren.
Bagging umgeht diesen Kompromiss, indem es die Varianz des instabilen Prädiktors reduziert, während der Bias weitgehend unbeeinflusst bleibt.
Methode
Insbesondere verwendet Bagging wiederholtes Bootstrap-Sampling, um mehrere Versionen desselben Vorhersagemodells (z. B. Regressionsbäume) zu erzeugen und mittelt über die resultierenden Vorhersagen.
Schauen wir uns im Detail an, wie Bagging funktioniert:
- Konstruiere eine Bootstrap-Stichprobe $(y_{i}^{}, \mathbf{x_{i}^{}}) : (i = 1, \dots , n)$ (mit Zurücklegen) aus den ursprünglichen i.i.d.-Daten $(y_{i}, \mathbf{x_{i}}) : (i = 1, \dots , n)$.
- Fitte einen Regressionsbaum auf die Bootstrap-Stichprobe – wir bezeichnen den Baumprädiktor mit $\hat{\theta}_{n}^{*}(\mathbf{x})$.
- Wiederhole Schritt 1 und 2 insgesamt $B$-mal und berechne $ \frac{1}{B}\sum_{b=1}^{B}\hat{\theta}_{n, b}^{*}(\mathbf{x})$.
OK – werfen wir einen Blick in die Konstruktionsphase: Es werden insgesamt $B$ verschiedene Bootstrap-Stichproben gleichzeitig aus den Originaldaten gezogen. Auf jede dieser Stichproben wird ein Baum gefittet und die (In-Sample-)Vorhersagen werden in Schritt 3 gemittelt, was den gebaggten Prädiktor ergibt.
Die Varianzreduktion erfolgt in Schritt 3. Um dies zu verdeutlichen, betrachten wir folgendes einfaches Beispiel:
Seien $X_1, \dots, X_n$ i.i.d. Zufallsvariablen mit $\mu = E[X_1]$ und $\sigma^2 = \text{Var}[X_1]$ und sei $\bar{X}= \frac{1}{n}\sum_{i=1}^{n}X_{i}$. Einfache Umformungen zeigen:
$\text{Var}[\bar{X}]=\frac{\sigma^2}{n} \leq \sigma^2$
$E[\bar{X}]=\mu$
Wir stellen fest, dass die Varianz des Mittelwertes tatsächlich schwächer als die der einzelnen Zufallsvariablen ist, während der Stichprobenmittelwert erwartungstreu ist.
Es wird in der Literatur viel diskutiert, warum Bagging funktioniert, und es bleibt eine offene Forschungsfrage. Bühlmann und Yu (2002) schlagen eine Subsampling-Variante des Bagging vor, genannt Subagging, die aus theoretischer Sicht besser nachvollziehbar ist.
Insbesondere ersetzen Bühlmann und Yu (2002) das Bootstrap-Verfahren im Bagging durch Subsampling ohne Zurücklegen. Im Wesentlichen ändern wir dabei nur Schritt 1 unseres Bagging-Algorithmus, indem wir $m$-mal ohne Zurücklegen zufällig aus unseren Originaldaten ziehen mit $m < n$ und so eine Teilmenge der Größe $m$ erhalten. Mit dieser Variante ist es möglich, obere Schranken für die Varianz und den mittleren quadratischen Fehler (MSE) des Prädiktors anzugeben, vorausgesetzt es wird eine geeignete Stichprobengröße $m$ gewählt.
Simulationsaufbau
Da die Theorie etwas umständlich ist und Kenntnisse in reeller Analysis erfordert, simulieren wir die zentralen Ergebnisse von Bühlmann und Yu (2002).
Wir vergleichen den mittleren quadratischen Vorhersagefehler (MSPE) des Regressionsbaums, des gebaggten und des subgebaggten Prädiktors und illustrieren dabei den theoretischen Teil ein wenig mehr.
Dazu betrachten wir folgendes Modell:
$$y_{i} = f(mathbf{x}_{i}) + epsilon_{i}$$
wobei $f(\mathbf{x}{i})$ die Regressionsfunktion ist, $\mathbf{x}{i} \sim U^{10}[0,1]$ die aus einer Gleichverteilung generierte Designmatrix ist und $\epsilon_{i} \sim N(0,1)$ der Fehlerterm ist ($\forall i = 1, \dots, n$).
Für den wahren Datenerzeugungsprozess (DGP) betrachten wir das folgende Modell, das in der Machine Learning-Literatur häufig verwendet wird und als „Friedman #1“-Modell bekannt ist:
$$f(mathbf{x}) = 10 sin(pi x^{(1)} x^{(2)}) + 20(x^{(3)} - frac{1}{2})^{2} + 10 x^{(4)} + 5 x^{(5)}$$
wobei $\mathbf{x}^{(j)}$ die $j$-te Spalte der Designmatrix $\mathbf{x}$ ist (für $1 \leq j \leq 10$).
Wie man sieht, ist dieses Modell stark nichtlinear – Regressionsbaum-Modelle sollten daher geeignet sein, unseren DGP zu approximieren.
Zur Bewertung der Vorhersageleistung der Bagging- und Subagging-Prädiktoren führen wir eine Monte-Carlo-Simulation in Python durch.
Wir importieren zunächst die relevanten Pakete.
<span class="hljs-keyword"><span class="hljs-keyword">import</span></span> numpy <span class="hljs-keyword"><span class="hljs-keyword">as</span></span> np
<span class="hljs-keyword"><span class="hljs-keyword">import</span></span> sklearn.model_selection
<span class="hljs-keyword"><span class="hljs-keyword">import</span></span> sklearn.ensemble
<span class="hljs-keyword"><span class="hljs-keyword">import</span></span> simulation_class
<span class="hljs-keyword"><span class="hljs-keyword">import</span></span> math
<span class="hljs-keyword"><span class="hljs-keyword">from</span></span> sklearn.metrics <span class="hljs-keyword"><span class="hljs-keyword">import</span></span> mean_squared_error
<span class="hljs-keyword"><span class="hljs-keyword">from</span></span> sklearn.tree <span class="hljs-keyword"><span class="hljs-keyword">import</span></span> DecisionTreeRegressor
Das Modul simulation_class ist eine benutzerdefinierte Klasse, die wir in diesem Blogbeitrag nicht besprechen werden, sondern in einem nachfolgenden.
Darüber hinaus spezifizieren wir das Simulations-Setup:
<span class="hljs-comment"><span class="hljs-comment"># Number of regressors</span></span>
n_reg = <span class="hljs-number"><span class="hljs-number">10</span></span>
<span class="hljs-comment"><span class="hljs-comment"># Observations</span></span>
n_obs = <span class="hljs-number"><span class="hljs-number">500</span></span>
<span class="hljs-comment"><span class="hljs-comment"># Simulation runs</span></span>
n_sim = <span class="hljs-number"><span class="hljs-number">50</span></span>
<span class="hljs-comment"><span class="hljs-comment"># Number of trees, i.e. number of bootstrap samples (Step 1)</span></span>
n_tree = <span class="hljs-number"><span class="hljs-number">50</span></span>
<span class="hljs-comment"><span class="hljs-comment"># Error Variance</span></span>
sigma = <span class="hljs-number"><span class="hljs-number">1</span></span>
<span class="hljs-comment"><span class="hljs-comment"># Grid for subsample size</span></span>
start_grid = <span class="hljs-number"><span class="hljs-number">0.1</span></span>
end_grid = <span class="hljs-number"><span class="hljs-number">1</span></span>
n_grid = <span class="hljs-number"><span class="hljs-number">100</span></span>
grid_range = np.linspace(start_grid, end_grid, num = n_grid)
Im Folgenden werden wir näher erläutern, wofür wir die Gitter-Spezifikation benötigen.
Um unsere Simulationsergebnisse zu speichern, richten wir Container ein.
<span class="hljs-comment"><span class="hljs-comment"># Container Set-up</span></span>
mse_temp_bagging = np.empty(shape = (n_obs, n_sim))
mse_temp_subagging = np.empty(shape = (n_obs, n_sim))
y_predict_bagging = np.empty(shape = (n_obs, n_sim))
y_predict_subagging = np.empty(shape = (n_obs, n_sim))
mse_decomp = np.empty(shape = (len(grid_range),<span class="hljs-number"><span class="hljs-number">2</span></span>))
Mit dieser Initialisierung erzeugen wir die Test- und Trainingsdaten mithilfe des simulation_class-Moduls.
<span class="hljs-comment"><span class="hljs-comment">#Creation of Simulation-Data</span></span>
train_setup = simulation_class.simulation(n_reg = n_reg,
n_obs = n_obs,
n_sim = n_sim,
sigma = sigma,
random_seed_design = <span class="hljs-number"><span class="hljs-number">0</span></span>,
random_seed_noise = <span class="hljs-number"><span class="hljs-number">1</span></span>)
test_setup = simulation_class.simulation(n_reg = n_reg,
n_obs = n_obs,
n_sim = n_sim,
sigma = sigma,
random_seed_design = <span class="hljs-number"><span class="hljs-number">2</span></span>,
random_seed_noise = <span class="hljs-number"><span class="hljs-number">3</span></span>)
f_train = train_setup.friedman_model()
X_train, y_train = train_setup.error_term(f_train)
f_test = test_setup.friedman_model()
X_test, y_test = test_setup.error_term(f_test)
Da wir die Daten für unser „Friedman #1“-Modell erzeugt haben, sind wir nun in der Lage, den mittleren quadratischen Fehler (mean squared error) des gebaggten Prädiktors und des subgebaggten Prädiktors zu simulieren. In Python sind beide Algorithmen über die Methode BaggingRegressor des sklearn.ensemble-Pakets implementiert. Beachte, dass wir für den Subagging-Prädiktor den Parameter max_samples im BaggingRegressor angeben müssen. Dies stellt sicher, dass wir eine Teilstichprobe der Größe $m = a \cdot n$ mit Teilstichprobenanteil $a$ aus den Originaldaten ziehen können. Tatsächlich haben wir für den Teilstichprobenanteil $a$ das Gitter bereits oben über die Variable grid_range spezifiziert.
<span class="hljs-comment"><span class="hljs-comment">#Subagging-Simulation</span></span>
<span class="hljs-keyword"><span class="hljs-keyword">for</span></span> index, a <span class="hljs-keyword"><span class="hljs-keyword">in</span></span> enumerate(grid_range):
<span class="hljs-keyword"><span class="hljs-keyword">for</span></span> i <span class="hljs-keyword"><span class="hljs-keyword">in</span></span> range(<span class="hljs-number"><span class="hljs-number">0</span></span>, n_sim):
<span class="hljs-comment"><span class="hljs-comment"># bagged estimator</span></span>
bagging = sklearn.ensemble.BaggingRegressor(
bootstrap = <span class="hljs-keyword"><span class="hljs-keyword">True</span></span>,
n_estimators = <span class="hljs-number"><span class="hljs-number">50</span></span>)
y_predict_bagging[:,i] = bagging.fit(
X_train,
y_train[:,i]).predict(X_test)
mse_temp_bagging[:,i] = mean_squared_error(
y_test[:,i],
y_predict_bagging[:,i])
<span class="hljs-comment"><span class="hljs-comment"># subagged estimator</span></span>
subagging = sklearn.ensemble.BaggingRegressor(
max_samples = math.ceil(a*n_obs),
bootstrap = <span class="hljs-keyword"><span class="hljs-keyword">False</span></span>,
n_estimators = <span class="hljs-number"><span class="hljs-number">50</span></span>)
y_predict_subagging[:,i] = subagging.fit(
X_train,
y_train[:,i]).predict(X_test)
mse_temp_subagging[:,i] = mean_squared_error(
y_test[:,i],
y_predict_subagging[:,i])
mse_decomp[index, <span class="hljs-number"><span class="hljs-number">1</span></span>] = np.mean(mse_temp_bagging)
mse_decomp[index, <span class="hljs-number"><span class="hljs-number">2</span></span>] = np.mean(mse_temp_subagging)
Auf meinem GitHub-Account findest du zusätzlichen Code, der auch den simulierten Bias und die Varianz für den vollständig wachsenden Baum und den gebaggten Baum berechnet.
Ergebnisse
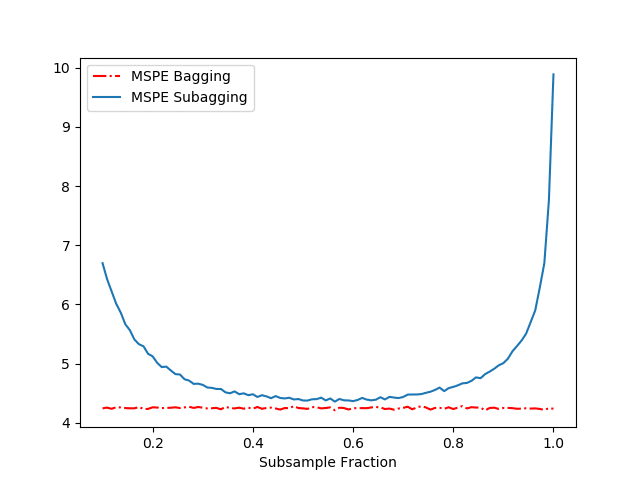
Die Ergebnisse unserer obigen Simulation sind in Abbildung 1 dargestellt.
Vergleichen wir zunächst die Leistung in Bezug auf den MSPE des Regressionsbaums und des gebaggten Prädiktors. Tabelle 1 zeigt uns, dass Bagging den MSPE drastisch reduziert, indem es die Varianz verringert, während der Bias nahezu unbeeinflusst bleibt. (Zur Erinnerung – der mittlere quadratische Prognosefehler ist einfach die Summe aus dem quadrierten Bias des Schätzers, der Varianz des Schätzers und der Varianz des Fehlerterms (nicht berichtet).)
Tabelle 1: Leistung des vollständig gewachsenen Baums und des gebaggten Prädiktors
Abbildung 1 zeigt den MSPE in Abhängigkeit vom Subsampling-Anteil $a$ für den gebaggten und subgebaggten Prädiktor (unser obiger Code). Zusammen mit Abbildung 1 und Tabelle 1 machen wir mehrere Beobachtungen:
- Wir sehen, dass sowohl der gebaggte als auch der subgebaggte Prädiktor einen einzelnen Baum übertreffen (in Bezug auf den MSPE).
- Für einen Subsampling-Anteil von ungefähr 0{,}5 erreicht Subagging nahezu die gleiche Prognoseleistung wie Bagging, jedoch bei geringeren Rechenkosten.
References
- Breiman, L.: Bagging predictors. Machine Learning, 24, 123–140 (1996).
- Bühlmann, P., Yu, B.: Analyzing bagging. Annals of Statistics 30, 927–961 (2002).


